Impossibility of Distributed Consensus with One Faulty Process (FLP Theorem)

TL;DR

1. 沒有任何一個fully asynchronous & fault tolerance protocol可以保證形成共識。
2. 在保證execution 的時候沒有process died & 在執行初始階段majority的processes都alive的情況下，有partially correct consensus protocol存在。

Term Definition

$Configuration$: $Configuration$ $C$代表所有$process$的internal state 加上 message buffer。

$Step$: $process$ $p$ 經過 event $e$ $=$ $(p, m)$，把$C$帶到下一個state，這稱為一個$step$。

$Schedule$: 從$C$開始，經過finite or infinite的events，把$C$帶到下一個configruation $C'$。

Lemmas

Lemma 1

兩個 schedule $\sigma_1$、$\sigma_2$，如果兩個 schedule disjoint，則順序不影響最終的結果 ($\sigma_1\sigma_2$ -> $C_3$, also $\sigma_2\sigma_1$ -> $C_3$)。

proof

兩者不interaction，所以根據系統定義，執行順序不影響結果。

Lemma 2

$P$會有一個bivalent initial configuration。($bivalent$: 最終結果的candidate有兩個)

proof

假設不存在bivalent initial configuration，所有的initial configuration執行完deciding schedule以後，應該都是univalent。

我們先把initial configuration先照process排序，在照value排序，則會有一個 $C_0$是$p$的value 為0,而相鄰的$C_1$是$p$的value為1，其餘proccess的value都相同。

我們現在執行一個deciding schedule，在這個deciding schedule中，$p$並沒有任何動作，因為是deciding schedule，根據假設所有的initial configuration執行完應該都要是univalent，因此either是0-valent或是1-valent。

但是讓$C_0$ 和 $C_1$執行結果以後，result configurations卻有0-valent和1-valent(因為$p$並沒有動作，所以value不會改變)，與假設矛盾，故可知假設錯誤，因此有一組bivalent initial configuration。

Lemma 3

假設$C$是一組bivalent configuration，$e$ $=$ $(p, m)$為一個可以跑在$C$的event，$Y$是所有 $C$ 不跑$e$可以reachable的 configuration set，而$D$ $=$ $e(Y)$，則$D$包含一組bivalent configuration。

proof

假設$D$不包含bivalent configuration，定義$C_0$與$C_1$是neighbor，如果$e(C_0)$經過一個step可以到$C_1$。

$Y$中必存在一組$C_0$, $C_1$使得 $D_i$ $=$ $e(C_0)$(i = 0, 1)，為了不搞混我們稱此event為$e'$，$e'$ $=$ $(p', m')$。

Case 1 $p'$ $!=$ $p$ 如果$p'$ $!=$ $p$，則根據 lemma 1，$D_0$ 應該等於 $D_1$，所以此狀況不可能。

Case 2 $p'$ $=$ $p$

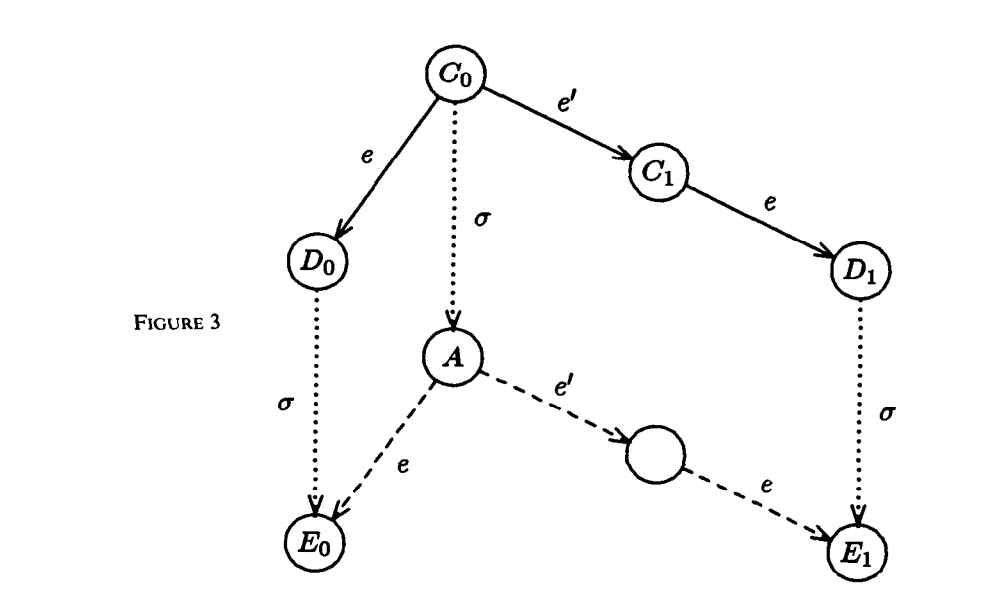如圖，定義一個deciding schedule使得$C$轉移到$A$，在由$A$各自轉移到$E_0$、$E_1$。根據lemma 1，執行的順序不影響結果，而$\sigma$是deciding schedule，所以$A$不會是導致變成bivalent的點，代表$D_0$、$D_1$導致了$E_0$、$E_1$，而$D$包含$D_0$、$D_1$，所以$D$是 bivalent，得證。

Theorems

Theorem 1

沒有任何一個fully asynchronous & fault tolerance protocol可以保證形成共識。

proof

假設$P$是fully asynchronous & fault tolerance且total correct，那必定存在一個deciding step使得最後達成consensus。

但根據lemma 2，一開始存在一組initial bivalent configuration，且根據lemma 1我們可以調換disjoint的event順序不影響結果，因此如果有fault發生我們可以先處理其他event並調換執行順序，因為fault會發生，而且process不知道其他process是掛了還是處理得很慢(因為asynchronous)，所以總是可以把deciding run往後延，先處理其他event。

在根據lemma 3，總是可以找到一個event使得result configruation是bivalent(沒有consensus)，所以證明protocol無法保證consensus，故不是total correct，得證。

Theorem 2

在保證execution 的時候沒有process died & 在執行初始階段majority的processes都alive的情況下，有partially correct consensus protocol存在。

proof

作者提出一個作法證明可以partially correct，故不用證明。

References

• https://ilyasergey.net/CS6213/week-03-bft.html#flp-theorem